6 Приложения
6.1 Банкови заеми
Банка е в процеса на определяне на кредитната си политика за пет различни сектора с характеристики дадени в следната таблица:
| Вид кредит | Лихва | Дял на несъбираеми кредити |
|---|---|---|
| Потребителски | 0.15 | 0.10 |
| Автомобили | 0.13 | 0.07 |
| Недвижими имоти | 0.12 | 0.03 |
| Земеделие | 0.125 | 0.05 |
| Търговия | 0.10 | 0.02 |
Банката разполага с общо 12 милиона лева и при определяне на политиката трябва да се съобрази със следните регулации:
- Поне 40% от заемите трябва да са насочени към търговския сектор.
- Заеми за недвижими имоти трябва да са поне половината от общата сума на потребителски кредити, кредити свързани с автомобили и недвижими имоти.
- По силата на регулаторни изисквания делът на несъбираемите кредити не трябва да надвишава 4% от всички кредити. Несъбираемите кредити не носят лихви.
Какъв е оптималният (най-висока печалба) план за банката?
6.2 Производство и склад (1)
Малък шивашки цех се опитва да определи производствения си план за следващия сезон. Цехът произвежда четири продукта: якета, шапки, ръкавици и панталони, които се произвеждат в четири отделения: рязане, уплътняване, шиене и пакетиране.
| Отделения/продукти | Якета | Шапки | Ръкавици | Панталони | Капацитет (часове) |
|---|---|---|---|---|---|
| Рязане | 0.3 | 0.3 | 0.25 | 0.15 | 1000 |
| Уплътняване | 0.25 | 0.35 | 0.3 | 0.10 | 1000 |
| Шиене | 0.45 | 0.5 | 0.4 | 0.22 | 1000 |
| Пакетиране | 0.12 | 0.15 | 0.1 | 0.05 | 1000 |
Цехът вече има получени поръчки за четирите продукта. Договорите за производство включват неустойка за всяка недоставена единица:
| Отделения/продукти | Якета | Шапки | Ръкавици | Панталони |
|---|---|---|---|---|
| Поръчки (брой) | 800 | 750 | 600 | 600 |
| Печалба (лв./брой) | 30 | 40 | 20 | 10 |
| Неустойка (лв./брой) | 15 | 20 | 10 | 8 |
Намерете оптималния производствен план за този цех.
6.3 Производство и склад (1)
Компания за производство на дограма има договор за доставка на дървени дограми за следващите 6 месеца. За същия период компанията очаква разходите за производство (труд и материали) да варират. Компанията може да се възползва от по-ниски производствени разходи в даден период и да произведе повече дограми от необходимото, като разходите за складиране на продуктите са 8 лв. на месец на брой. В момента на планиране фирмата няма готови дограми на склад.
| Януари | Февруари | Март | Април | Май | Юни | |
|---|---|---|---|---|---|---|
| Поръчки (брой) | 100 | 250 | 190 | 140 | 220 | 110 |
| Производствени разходи (лв./брой) | 50 | 45 | 55 | 48 | 52 | 50 |
Формулирайте оптимизационна задача, която да намери оптималния производствен план.
6.4 Производство и персонал (1)
Компания за производство на дограма има договор за доставка на дървени дограми за следващата година. Компанията разполага с 10 опитни сътрудника, назначени на трудови договори. Всеки от тях произвежда по 12 дограми на тримесечие. Компанията може да отговори на флуктуациите в търсенето на своите продукти, като назначава и уволнява сътрудници на срочни договори. Временно заетите произвеждат по 3 дограми на месец. Разходите за назначаване/уволняване на временни сътрудници са съответно 200 лв. и 400 лв. за тримесечие. Компанията може да складира непродадени единици на цена 50 лв. на месец на единица.
| Януари-Март | Април-Юни | Юли-Септември | Октомври-Декември | |
|---|---|---|---|---|
| Поръчки (брой) | 520 | 720 | 520 | 620 |
Формулирайте оптимизационна задача, която да намери оптималния план за назначаване/уволняване на временно заетите работници.
6.5 Производство и персонал (2)
Фирма, специализирана в производство на зимни палта се опитва да посрещне търсенето на нейните стоки с възможно най-малки разходи. Всеки работник, нает в началото на сезона работи през целия сезон, произвежда 80 палта и получава 6000 лв. заплата. В началото на годината фирмата разполага с 30 работника.
Търсенето на палта има силни сезонни колебания и фирмата има три опции, за да отговори на тези вариации:
- работниците могат да работят и по-продължително, но допълнителният труд се заплаща 50% по-скъпо и работниците могат да работят не повече от 20% повече от нормалното работно време.
- Произведени в предишния период палта могат да се складират на цена от 12 лв. на сезон за всяко палто.
- Фирмата може да назначава и освобождава служители. За назначаване на един нов служител цената е 500 лв. За освобождаване на служител разходите възлизат на 420 лв.
- Фирмата няма начални запаси от готови палта.
Маркетинговият отдел на предприятието оценява, че през следващите четири сезона търсенето ще възлиза на съответно 5000, 2000, 500 и 1500 палта.
Изгответе математически модел с който да намерите оптималния план (в смисъл на най-ниски разходи) за тази фирма.
\[\begin{align*} & w_i: \text{работници в сезон } i\\ & x_i: \text{произведени палта в сезон } i\\ & o_i: \text{произведени с извънреден труд палта в сезон } i\\ & h_i: \text{брой наети сътрудници в сезон } i\\ & f_i: \text{брой освободени сътрудници в сезон } i\\ & s_i: \text{брой палта на склад сезон } i\\ & d_i: \text{брой палта продадени през сезон } i\\ \end{align*}\]
\[\begin{align*} & \min 6000 \sum_{i = 1}^{4} w_i + 500 \sum_{i = 1}^{4} h_i + 420 \sum_{i = 1}^{4} f_i + 12 \sum_{i = 1}^{4} s_i + 1.5\frac{6000}{80} \sum_{i = 1}^{4} o_i\\ & w_0 = 30\\ & w_i = w_{i - 1} + h_i - f_i\\ & x_i = 80 w_i + o_i \\ & s_0 = 0 \\ & s_i = s_{i - 1} + x_i - d_i \\ & o_i \leq 0.2 \cdot 80 w_i \end{align*}\]
6.6 Планиране на работни смени
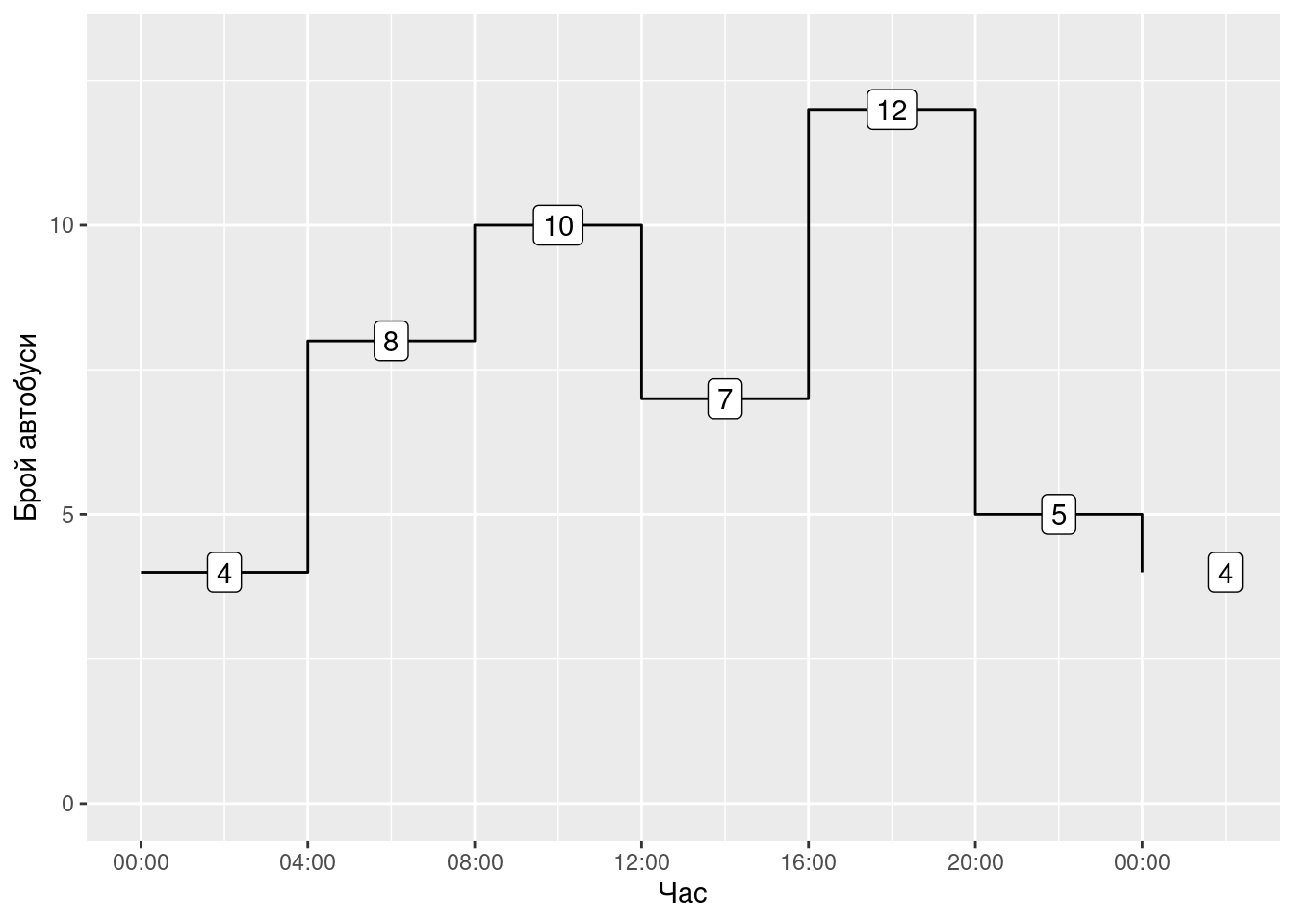
Да си представим, че община София разработва разписанието на нова автобусна линия. Изследване на търсенето по маршрута на тази линия показва колко автобуси трябва да обслужват линията в 6 часови диапазона (Фигура 6.1). Всеки автобус може да започне смяна в 00:01, 04:01, 08:01, 12:01, 16:01 или в 20:01 обслужва линията в продължение на 8 часа. Намерете най-малкия брой автобуси, които са нужни за обслужването на линията.
6.7 Радиотерапия
| Лъч 4 | Лъч 5 | Лъч 6 | |
|---|---|---|---|
| Лъч 1 | 1/1 | 2/1 | 2/1 |
| Лъч 2 | 1/2 | 2/2 | 2.5/2 |
| Лъч 3 | 1.5/1 | 1.5/1 | 2.5/1 |
Целата е здравите тъкани (в зелено) да получат възможно най-малка доза радиация, докато в същото време болните тъкани трябва да получат поне 7Gy (Грей), за да бъдат унищожени. Тъканта на гръбначния мозък (в синьо) е особено чувствителна и не трябва да бъде изложена на радиация повече от 5Gy.
\[\begin{align*} & \min (x_1 + x_4) + (2x_2 + 2x_5) + (2x_1 + x_6) + (2.5x_3 + x_6) = \\ 3x_1 + 2x_2 + 2.5x_3 + 2x_6 \\ & x_2 + 2x_4 \geq 7\\ & 1.5x_3 + x_4 \geq 7 \\ & 2x_1 + x_5 \geq 7 \\ & 1.5x_3 + x_5 \geq 7 \\ & 2.5x_2 + 2x_6 \geq 7 \\ & 2x_2 + 2x_5 \leq 5 \end{align*}\]
6.8 Планиране на градско строителство
Да приемем, че София е изправена пред дефицит в местния бюджет и общинският съвет обмисля как да увеличи приходите от данък сгради чрез преустройства на общински имоти. Проектът се състои от две части – разчистване на занемарени и повредени постройки и построяване на нови жилища.
- В момента на планиране общината притежава 300 занемарени постройки, които могат да бъдат съборени. Всеки от тях освобождава 1000 кв. метра и събарянето й струва 3 000 лв. на постройка. 15 процента от освободеното пространство е предвидено за улици, тротоари и свободни пространства.
- На освободените парцели общината може да построи четири вида нови жилищни сгради: еднофамилни (300 кв. метра), двуфамилни (500 кв. метра), три-фамилни (700 кв. метра) и четири-фамилни къщи (900 кв. метра). Очакваните данъчни постъпляния са съответно 1 000 лв., 1 700 лв., 2 400 лв. и 2 800 лв. на година.
- Поне 20 процента от новите постройки трябва да са еднофамилни къщи, двуфамилните домове трябва да съставляват поне 20 процента, а три и четири-фамилните домове трябва да са поне една четвърт от всички нови постройки.
- Строителните разходи за новите домове са съответно 50 000 лв., 70 000 лв., 130 000 лв. и 160 000 лв.
- Общината предвижда на финансира проекта чрез банков заем, който не може да надвишава 15 милиона лева.
Колко от всеки вид къщи трябва да планира да построи общината, така че да постигне възможно най-високи данъчни постъпления?
6.8.1 Математически модел
Целеви променливи: \(x_1\) (брой еднофамилни къщи), \(x_2\) (брой двуфамилни къщи), \(x_3\) (брой трифамилни къщи), \(x_4\) (брой четирифамилни къщи), \(x_4\) (брой съборени стари постройки).
Целева функция (очаквани годишни данъчни постъпления):
\[ \max z = 1000 x_1 + 1700 x_2 + 2400 x_3 + 2800 x_4 \]
Ограничения:
- Общо застроената площ трябва да е не по-голяма от освободената:
\[ 300 x_1 + 500 x_2 + 700 x_3 + 900 x_4 \leq (1 - 0.15)\cdot 1000 x_5 \]
Броят съборени постройки не може да надвишава 300: \[ x_5 \leq 300 \]
Изисквания за новите домове:
\[\begin{align*} x_1 \geq 0.2 \sum_{i = 1}^4 x_i \\ x_2 \geq 0.2 \sum_{i = 1}^4 x_i \\ x_3 + x_4 \geq 0.25 \sum_{i = 1}^4 x_i \end{align*}\]
- Бюджетно ограничение
\[ 50 x_1 + 70 x_2 + 130 x_3 + 160 x_4 + 3 x_5 \leq 15000 \]
6.8.2 Решение
Решение в Excel можете да изтеглите от тук.
/home/amarov/anaconda3/lib/python3.9/site-packages/pulp/pulp.py:1352: UserWarning: Spaces are not permitted in the name. Converted to '_'
warnings.warn("Spaces are not permitted in the name. Converted to '_'")1Model Status:OptimalObjective = 314.3115937Demolished = 108.69565
Double = 99.637681
Quadruple = 0.0
Super = 36.231884
Triple = 45.289855Constraint: Area, shadow price: 7.3955669e-05, slack -0.0
Constraint: Demolitions, shadow price: -0.0, slack 191.30435
Constraint: Single, shadow price: 0.26612674, slack 3.5527137e-15
Constraint: Double, shadow price: -0.0, slack 81.521739
Constraint: Triple/Quadruple, shadow price: 0.57203751, slack -0.0
Constraint: Budget, shadow price: 0.020954106, slack -0.0Solution time: 0.00000000 secondsСъщата задача, но с целеви променливи в множеството на целите (неотрицателни) числа.
1Model Status:OptimalObjective = 313.49999999999994Demolished = 109.0
Double = 99.0
Quadruple = 3.0
Super = 36.0
Triple = 42.0Constraint: Area, shadow price: -0.0, slack 250.0
Constraint: Demolitions, shadow price: -0.0, slack 191.0
Constraint: Single, shadow price: -0.0, slack -1.7763568e-15
Constraint: Double, shadow price: -0.0, slack 81.0
Constraint: Triple/Quadruple, shadow price: -0.0, slack -0.0
Constraint: Budget, shadow price: -0.0, slack 3.0
Constraint: _C1, shadow price: -0.0, slack 3.0Solution time: 0.0116 seconds6.9 Оптимизация на производство (рафинерия)
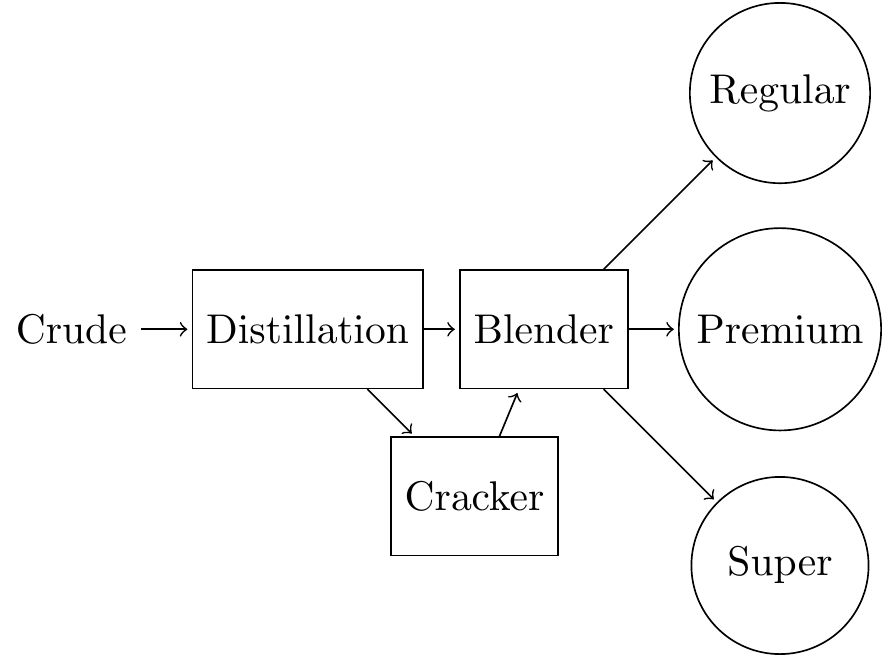
Рафинерия произвежда три вида безоловен бензин, които се различават по октановото си число (ON): обикновен (\(ON \geq 87\)), премиум (\(ON \geq 89\)) и супер (\(ON \geq 92\)). Преработката на суровия петрол обхваща три компонента.
- В първият компонент суровият петрол се дестилира до петролна суровина (feedstock) с октаново число ON = 82. За производството на един барел суровина са нужни 5 барела суров петрол. Капацитетът на дестилационните съоръжения са 1 500 хиляди барела на ден.
- Част от петролната суровина се обработва допълнително в термичен крекер, който произвежда бензин с ON = 98. От един барел суровина крекерът произвежда половин барел бензин. Капацитетът на крекера е ограничен до 200 000 барела петролна суровина на ден.
- Последният елемент в рафинерията е смесител, който комбинира бензин от крекера и петролната суровина от дестилацията. Октановото число на смес е приблизително равно на претегленото средно на октановите числа компонентите й.
- Търсенето на трите вида бензин е ограничено до съответно 50, 30, и 40 хиляди барела на ден.
- Рафинерията оценява печалбата от барел бензин на съответно 6, 7 и 8 долара за трите вида бензи, които продава.
Съставете математически модел, на базата на който да препоръчате оптимален (най-висока печалба) производствен план на рафинерията.
6.10 График за изпълнение на проекти
Софийска община планира четири строителни проекта за жилищни сгради между 2024 и 2028 г. Всеки проект има различна начална година и срок за изпълнение, описани в следващата таблица.
| Проект/Година | 2024 | 2025 | 2026 | 2027 | 2028 | Разход | Годишен приход |
|---|---|---|---|---|---|---|---|
| Проект 1 | Начало | Край | 5.0 | .05 | |||
| Проект 2 | Начало | Край | 8.0 | .07 | |||
| Проект 3 | Начало | Край | 15.0 | .15 | |||
| Проект 4 | Начало | Край | 1.2 | .02 | |||
| Бюджет | 3.0 | 6.0 | 7.0 | 7.0 | 7.0 |
Проекти 1 и 4 трябва да бъдат налъпно завършени в срок. Останалите два проекта могат да бъдат и частично завършени към края на срока, но всички проекти трябва да са завършени поне до 1/4 в края на срока им. В края на всяка година в завършената част на проктите се нанасят наематели и започват да плащат наем, пропорционален на степента на завършеност на проекта. Пример: ако при проект 1 през 2024 г. са изпълнени 40%, а останалите 60% са изпълнени към края на 2026 година. Oбщият доход от този проект за периода от пет години ще е \(0.4 \cdot 0.5 \cdot 50000\) за първата година, също толкова за втората и третата година, \((0.4 + 0.6) \cdot 50000\) през четвъртата и през петата година. Разходите за всеки проект се разпределят правопропорционално на степента на изпълнение за всяка година и общите разходи не могат да надвишават бюджетните ограничения за всяка година. Всички стойности са дадени в милиони лв.
Съставете математически модел за графика на изпълнение на проектите. Целта е да се намери графикът (ако съществува) с най-голям общ приход за петте годишни. За целите на задачата приемете, че 1 лв. през 2024 е равен на 1 лв. и през следващите четири години.
6.11 Задача
Компания произвежда три вида зърнени закуски: A, B и C. Закуските се произвеждат от четири съставки: овесени ядки, стафиди, настъргани кокосови орехи и нарязани бадеми. Продукт А е смес от овесени ядки, стафиди и бадеми в съотношение 50:5:2. Продукт B е смес от овесени ядки, кокос и бадеми в съотношение 60:2:3, а в продукт C са смесени овесени ядки, стафиди, кокос и бадеми в пропорция 60:3:4:2. Компанията продава продуктите за съответно 2.00 лв., 2.50 лв. и 3 лв. за кутия от 2 кг. Компанията се стреми да задоволи минимално дневно търсене на A, B и C от 500, 600 и 400 кутии. Компанията купува съставките за 100 лв./тон (овесени ядки), 120 лв./тон (стафиди), 110 лв./тон (кокос) и 200 лв./тон (бадеми). Доставките са ограничени до 5 тона на ден (овесени ядки), 2 тона (стафиди) и по един тон на ден за останалите две съставки (кокос, бадеми).
Съставете математически модел с който да препоръчате оптимален производствен план за тази компания. Целта на модела е да немери план с най-висока стойност на печалбата на компанията.
Нека \(x_1\), \(x_2\) и \(x_3\) са произведените количества (в тонове) от закуските A, B и C. Целевата функция е печалбата на компанията. Печалбата е разликата между приходи и разходи. Както приходите, така и разходите зависят от количествата произведени продукти.
\[ z(x_1, x_2, x_3) = \text{приходи}(x_1, x_2, x_3) - \text{разходи}(x_1, x_2, x_3) \]
Приходната част на целевата функция се вижда директно от цените на закуските. Тъй като цените са дадени за кутии от 2 кг., а количествата продукти са изразени в тонове, умножаваме количествата по 500 кутии/тон (един тон закуски съответства на 500 кутии от по 2 кг.).
\[ \text{приходи}(x_1, x_2, x_3) = 500 \cdot 2.00 x_1 + 500 \cdot 2.50x_2 + 500 \cdot 3x_3 = 500(2.00 x_1 + 2.50x_2 + 3x_3) \]
Разходната част на целевата функция се формира от количествата съставки (овесени ядки, стафиди и т.н.), които се използват за производството на \(x_1, x_2, x_3\) тона от закуските. За да определим количествата използвани съставки разглеждаме формулите за производство. От информацията за пропорциите на съставките в продукт A разбираме, че от общо 50 + 5 + 2 = 57 части 50 от тях са овесени ядки, 5 са стафиди, а 2 – бадеми. Това означава, че в един тон A 50/57 тона са овесени ядки, 5/57 тона са стафиди, а 2/57 тона са бадеми. Правим същите разсъждения и за останалите два продукта и получаваме следната таблица.
| Продукт/Съставка | Ов. ядки | Стафиди | Кокос | Бадеми |
|---|---|---|---|---|
| A | \(\frac{50}{57}\) | \(\frac{5}{57}\) | \(0\) | \(\frac{2}{57}\) |
| B | \(\frac{60}{65}\) | \(0\) | \(\frac{2}{65}\) | \(\frac{3}{65}\) |
| C | \(\frac{60}{69}\) | \(\frac{3}{69}\) | \(\frac{4}{69}\) | \(\frac{2}{69}\) |
От таблицата разбираме, че ако произведем един тон A ще изразходваме \(50/57\) тона овесени ядки. При един произведен тон B ще изразходваме \(50/65\) тона овесени ядки, а при един произведен тон C ще изразходваме \(60/69\) тона овесени ядки. Общият разход (в тонове) на овесени ядки при произведени \(x_1, x_2, x_3\) от продуктите е даден от
\[ \text{разход ов. ядки}(x_1, x_2, x_3) = \frac{50}{57} x_1 + \frac{60}{65} x_2 + \frac{60}{69} x_3 \]
По същия начин определяме разходите (в тонове) на останлите три съставки
\[\begin{align*} & \text{разход стафиди}(x_1, x_2, x_3) = \frac{5}{57} x_1 + 0 \cdot x_2 + \frac{3}{69} x_3\\ & \text{разход кокос}(x_1, x_2, x_3) = 0 \cdot x_1 + \frac{2}{65} x_2 + \frac{4}{69} x_3\\ & \text{разход бадеми}(x_1, x_2, x_3) = \frac{2}{57} x_1 + \frac{3}{65} x_2 + \frac{2}{69} x_3 \end{align*}\]
Разходите в лв. за тези съставки като функция от \(x_1, x_2, x_3\) са
\[\begin{align*} \text{разходи (лв.)}(x_1, x_2, x_3) = & 100 \cdot \text{разход ов. ядки}(x_1, x_2, x_3) + \\ & 120 \cdot \text{разход стафиди}(x_1, x_2, x_3) + \\ & 110 \cdot \text{разход кокос}(x_1, x_2, x_3) + \\ & 200 \cdot \text{разход бадеми}(x_1, x_2, x_3) \end{align*}\]
За целевата функция получаваме
\[\begin{align*} z(x_1, x_2, x_3) = & 500(2.00 x_1 + 2.50x_2 + 3x_3) \\ & - 100\left(\frac{50}{57} x_1 + \frac{60}{65} x_2 + \frac{60}{69} x_3\right)\\ & - 120\left(\frac{5}{57} x_1 + \frac{3}{69} x_3\right) \\ & - 110\left(\frac{2}{65} x_2 + \frac{4}{69} x_3\right) \\ & - 200\left(\frac{2}{57} x_1 + \frac{3}{65} x_2 + \frac{2}{69} x_3\right) \end{align*}\]
В задачата са дадени ограничения за количествата съставки, които компанията може да си набави:
\[\begin{align*} & \text{разход ов. ядки}(x_1, x_2, x_3) \leq 5 \\ & \text{разход стафиди}(x_1, x_2, x_3) \leq 2 \\ & \text{разход кокос}(x_1, x_2, x_3) \leq 1 \\ & \text{разход бадеми}(x_1, x_2, x_3) \leq 1 \\ \end{align*}\]
Също така има изисквания за минимални количества произведени продукти. Тъй като тези ограничения са изразени в брой кутии, а \(x_1, x_2, x_3\) са количества в тонове, умножаваме количествата по 500 (кутии на тон), за да получим съвместими мерни единици.
\[\begin{align*} & 500 \cdot x_1 \geq 500 \\ & 500 \cdot x_2 \geq 600 \\ & 500 \cdot x_3 \geq 400 \end{align*}\]
6.12 Оптимизация на портфейл от активи
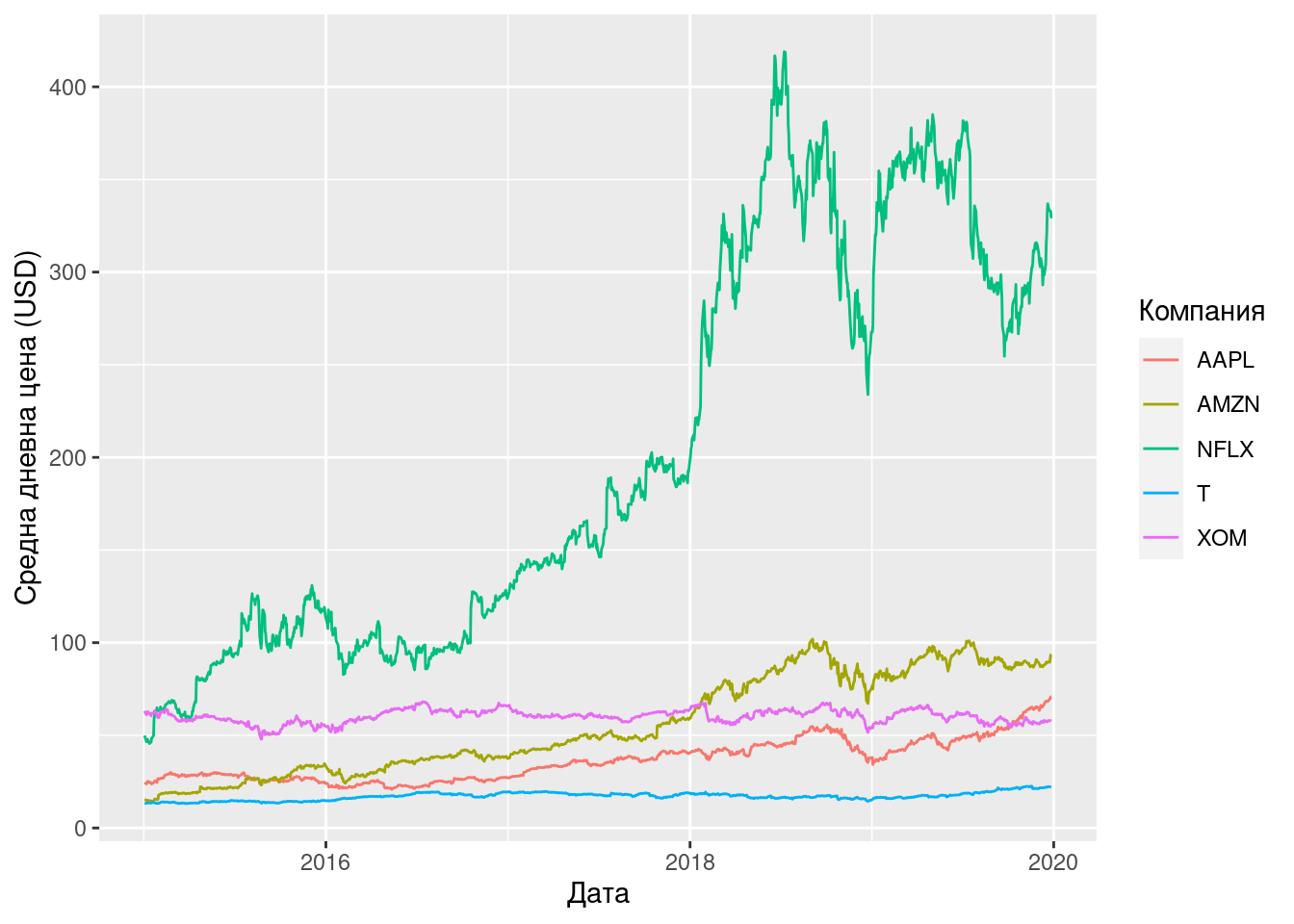
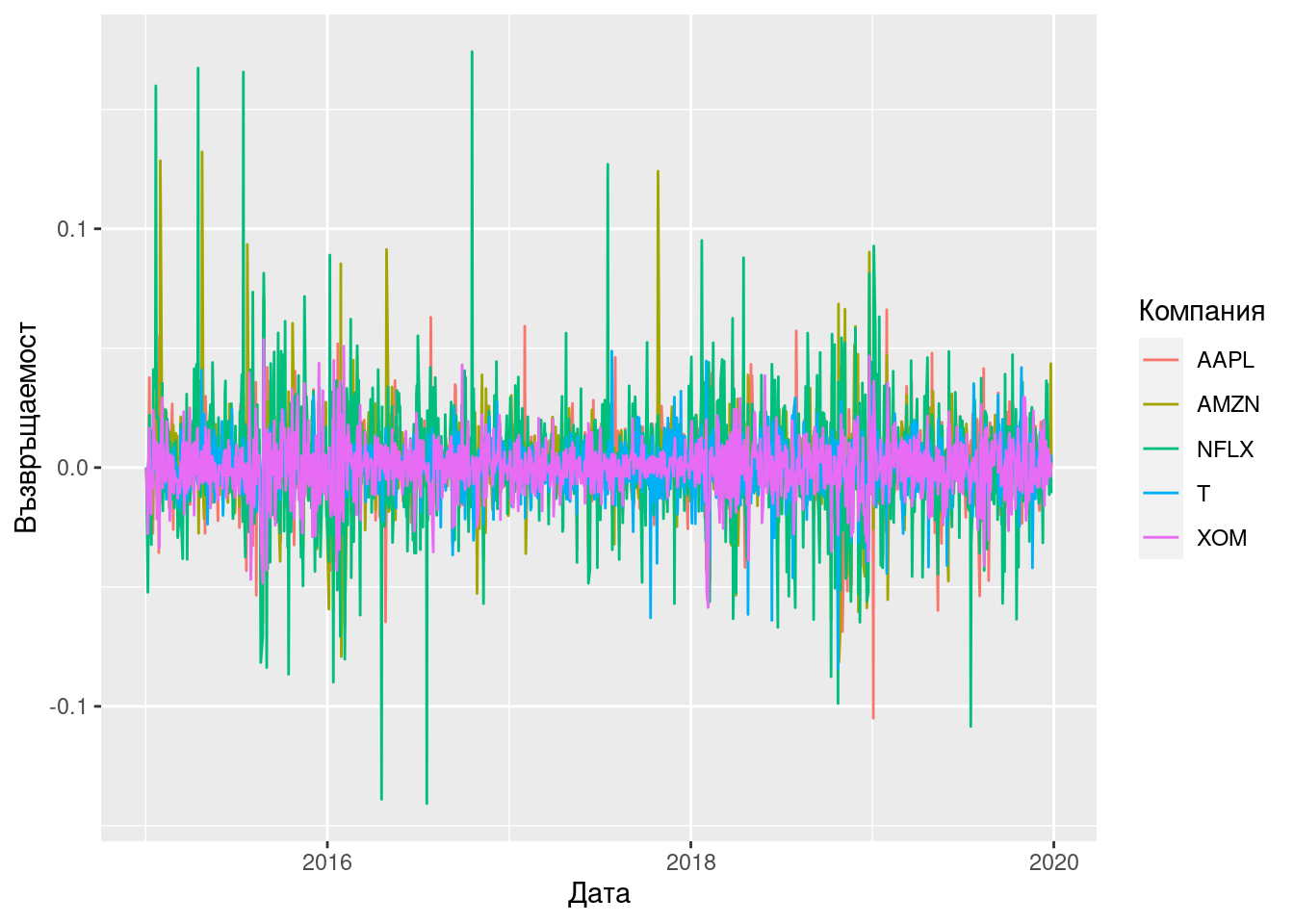
Да разгледаме 5 акции, търгувани на борсата: AMZN, AAPL, NFLX, XOM, T през периода от 2015-01-01 до 2019-12-30. Фигура 6.2 показва историята на цените на тези акции, а графика @ref(fig:portfolio-daily-returns) изобразява възвръщаемостта им на дневна база.
AAPL AMZN NFLX T XOM
0.00084 0.00143 0.00150 0.00041 -0.00007 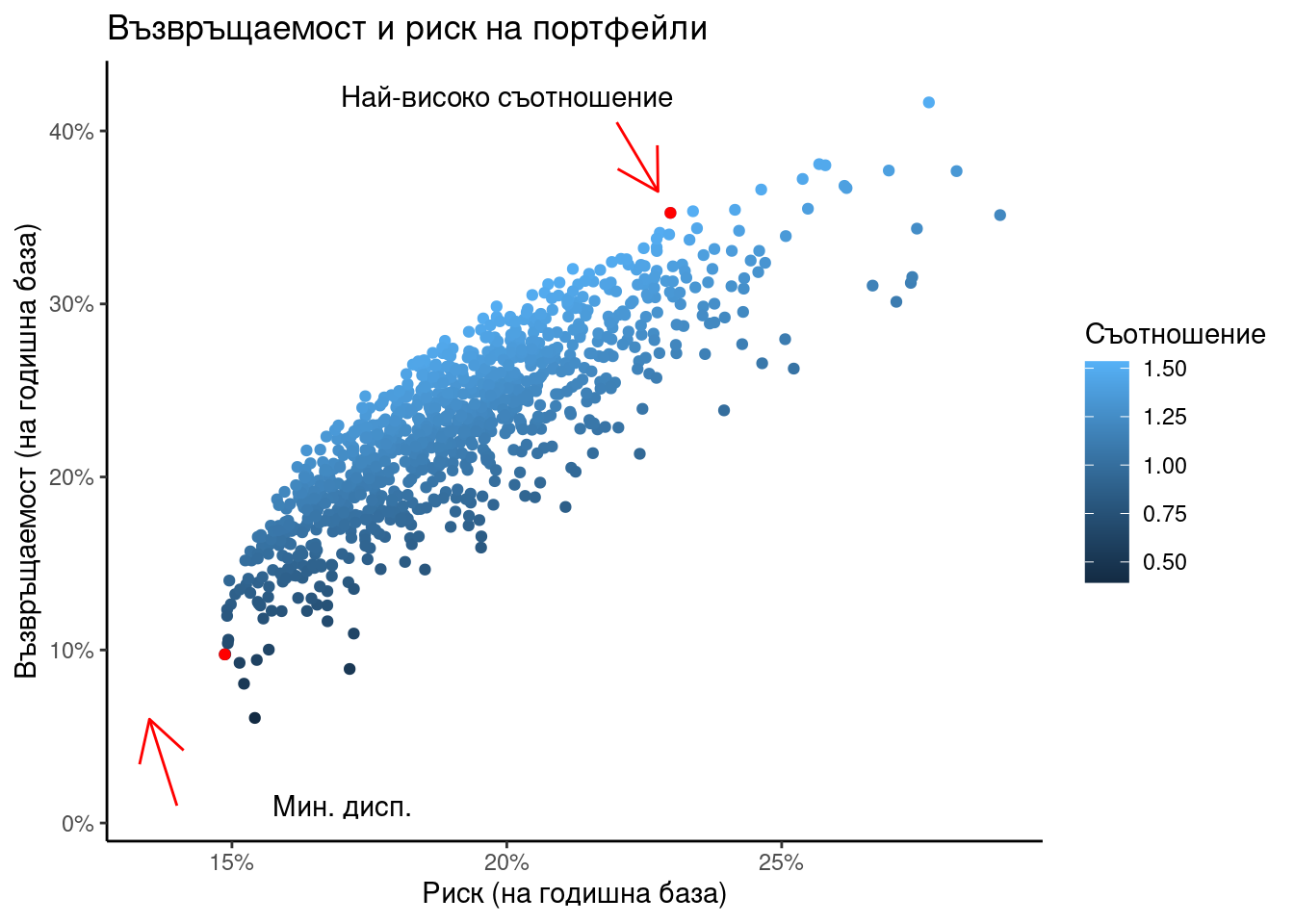

Тегла на портфейла с най-високо съотношение
Нека \(x = (x_1, x_2, \ldots, x_J)\) са тегла на \(J\) актива в портфейла. Да обозначим възвръщаемостта на актив \(j\) в период \(t\) с \(R_j(t)\), \(t = 1,\ldots, T\).
Възвръщаемостта на портфейла в период \(t\) е:
\[ R_x(t) = \sum_j x_j R_j(t) \]
Средната (историческа) възвръщаемост на портфейла \(x\) е дадена от
\[ \bar{R}_x = \frac{1}{T} \sum_{t = 1}^{T} R_x(t) \]
Рискът на портфейла \(x\) е даден от:
\[\begin{align*} \text{Risk}(x) & = \frac{1}{T} \sum_{t = 1}^{T}\left( R_x(t) - \bar{R}_x \right)^2 \\ & = \frac{1}{T} \sum_{t = 1}^{T}\left( \sum_j x_j R_j(t) - \frac{1}{T}\sum_{s = 1}^{T}\sum_j x_j R_j(s)\right)^2 \\ & = \frac{1}{T} \sum_{t = 1}^{T} \left( \sum_j x_j \left( R_j(t) - \frac{1}{T} \sum_{s = 1}^{T} R_j(s)\right) \right)^2 \\ & = \frac{1}{T} \sum_{t = 1}^{T} \left( \sum_j x_j \left(R_j(t) - \bar{R}_j \right)) \right)^2 \end{align*}\]
Оптимизационна задача:
\[\begin{align*} \max \frac{1}{T} \sum_{t = 1}^T \sum_j x_j R_j(t) \\ \frac{1}{T} \sum_{t = 1}^T \left| \sum_j x_j (R_j(t) - \bar{R}_j) \right| \leq \mu \end{align*}\]
Това не е линейна задача, тъй като ограниченията включват абсолютнати стойности. Нека
\[ y_t = \left| \sum_j x_j (R_j(t) - \bar{R}_j)\right| \]
Тогава задачата ще изглежда по следния начин:
\[\begin{align*} \max \frac{1}{T} \sum_{t = 1}^T \sum_j x_j R_j(t) \\ \left| \sum_j x_j (R_j(t) - \bar{R}_j)\right| = y_t \quad \text{за всяко } t\\ \frac{1}{T} \sum_{t = 1}^{T} y_t \leq \mu \\ \sum_j x_j = 1\\ x_j \geq 0 \quad \text{за всяко } j \end{align*}\]
\[\begin{align*} -y_i \leq \sum_j x_j (R_j(t) - \bar{R}_j) \leq y_i \end{align*}\]
6.13 Networks
TODO