2  Графичен метод

2.1 Задача: планиране на производство

Бутиково кафене в София предлага два продукта: Супер еспресо и Делукс еспресо. За приготвянето на един килограм от първия вид кафе са необходими по равни части бразилско и кубинско кафе, а рецептата за Делукс предвижда смес от бразилско и кубинско кафе в пропорция 1 към 3. Доставчиците са готови да осигурят 120 кг бразилско и 160 кг. кубинско кафе. Заведението знае, че няма да може да продаде повече от 150 кг. Делукс еспресо. От всеки продаден килограм Супер еспресо заведението печели 40 лв., докато печалбата от килограм Делукс възлиза на 50 лв.

Колко от двата типа кафе ще препоръчате на кафенето да смеси?

2.2 Математически модел

Целеви променливи:

\[ \begin{align*} & x_1: \text{ Супер еспресо (кг.)}\\ & x_2: \text{ Делукс еспресо (кг.)} \end{align*} \]

\[ \max z = 40 x_1 + 50 x_2 \text{ (целева функция)} \] \[\begin{align*} 0.5 x_1 + 0.25 x_2 & \leq 120 \text{ (бразилско кафе)}\\ 0.5 x_1 + 0.75 x_2 & \leq 160 \text{ (кубинско кафе)} \\ 0 \cdot x_1 + x_2 & \leq 150 \text{ (търсене Делукс)}\\ x_1 & \geq 0 \\ x_2 & \geq 0 \end{align*}\]

2.3 Допустимо множество

Както и в предишната задача ще изобразим графично допустимото множество, като начертаем правите, към всяко от петте неравенства:

\[\begin{align} 0.5 x_1 & + 0.25 x_2 & = & 120 \label{eq:p-2-constr-brazilian} \\ 0.5 x_1 & + 0.75 x_2 & = & 160 \label{eq:p-2-constr-cuban} \\ 0 \cdot x_1 & + x_2 & = & 150 \label{eq:p-2-constr-demand} \end{align}\]

Първо ще пресметнем пресечните точки на трите прави с осите \(x_1\) и \(x_2\)?

• Права бразилско кафе: (0, 120 / 0.25 = 480), (120 / 0.5 = 240, 0)
• Права кубинско кафе: (0, 160 / 0.75), (160 / 0.5, 0)
• Права търсене на Делукс: (0, 150), (100, 150) Тази права е успоредна на оста \(x_1\).

Фигура 2.1: Прави на ограниченията и допустимо множество.

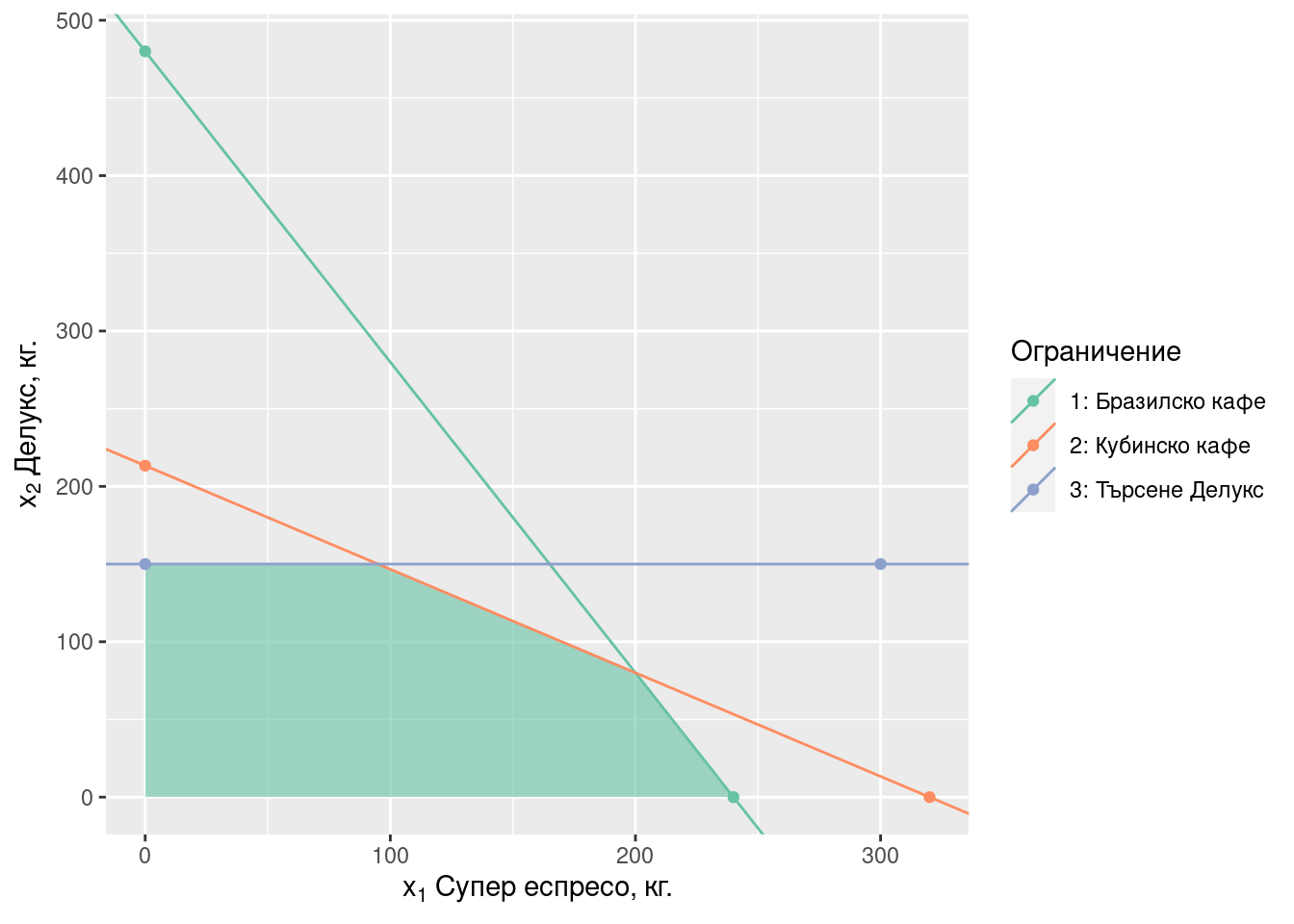
Допустимото множество е определено от всички точки, които едновременно изпълняват всички ограничения. На Фигура 2.1 това е полигонът определен от

1. Пресечната точка на равенствата на двете ограничения за неотрицателност: (0, 0)
2. Пресечната точка на неотрицателността на “Супер еспресо” (оста \(x_1\)) и “бразилско кафе”: (240, 0).
3. Пресечната точка на равенствата на ограниченията “бразилско кафе” и “кубинско кафе”
4. Пресечната точка на равенствата на ограниченията “кубинско кафе” и “търсене на Делукс”
5. Пресечната точка на равенствата на ограниченията “търсене на Делукс” и неотрицателността на Делукс (оста \(x_2\)). Вече пресметнахме тази точка, когато чертахме правите към ограниченията: (0, 150).

В пресечната точка на правите към “кубинско кафе”/“бразилско кафе” са изпълнени и двете равенства едновременно. За да намерим точката трябва да решим система от двете уравнения

\[ \begin{equation} \left | \begin{array}{@{}l@{}} 0.5 x_1 + 0.25 x_2 & = 120 \text{ (1: бразилско кафе)} \\ 0.5 x_1 + 0.75 x_2 & = 160 \text{ (2: кубинско кафе)} \end{array}\right.\,. \end{equation} \]

Един начин да решим системата е да извадим първото уравнение от второто уравнение. Когато го направим получаваме

\[ \begin{align} (0.75 - 0.25) x_2 & = 160 - 120 \\ 0.5 x_2 & = 40 \\ x_2 & = 80 \end{align} \]

Заместваме с \(x_2 = 80\) в първото уравнение и получаваме

\[ \begin{align} 0.5 x_1 + 0.25 \cdot 80 & = 120\\ x_1 & = 200. \end{align} \]

Решението на системата е (200, 80): пресечната точка на двете прави.

За да намерим координатите на пресечната точка на равенствата на “кубинско кафе” и “търсене на Делукс” трябва да решим системата от две уравнения принадлежащи към тези ограничения:

\[ \begin{equation} \left | \begin{array}{@{}l@{}} 0.5 x_1 + 0.75 x_2 & = 160 \text{ (2: кубинско кафе)} \\ 0\cdot x_1 + x_2 & = 150 \text{ (3: търсене делукс)} \end{array}\right.\,. \end{equation} \]

Решението на системата можем да получим, като заместим в първото уравнение с \(x_2 = 150\), за да получим

\[ \begin{equation} \left | \begin{array}{@{}l@{}} 0.5 x_1 + 0.75 \cdot 150 = 160 \implies 0.5x_1 = 160 - 112.5 \implies x_1 = 95 \\ x_2 = 150 \end{array}\right.\,. \end{equation} \]

С това намерихме координатите на пресечната точка между правите на “кубинско кафе” и “търсене на Делукс”: (95, 150).

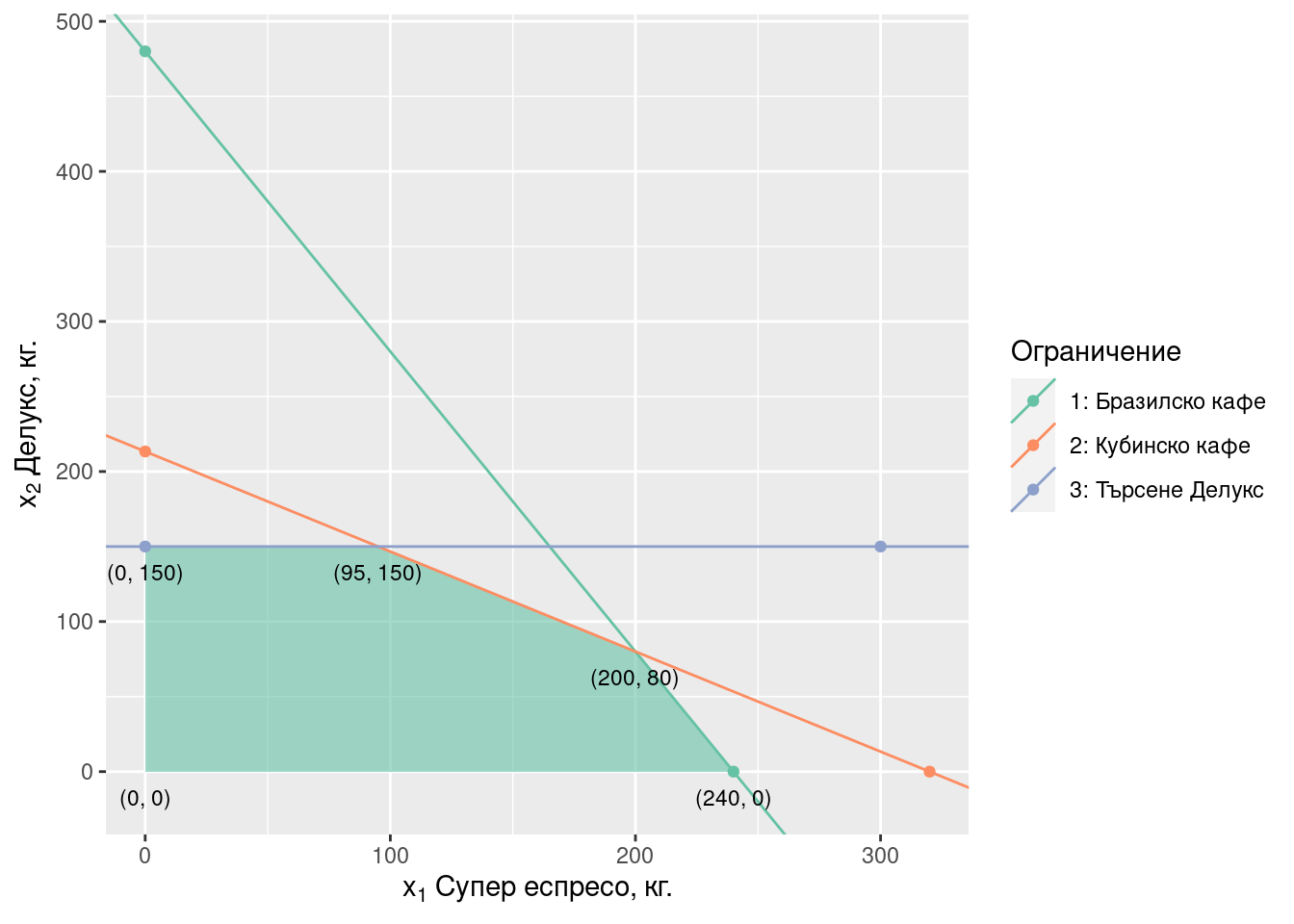
Така получаваме върховете на допустимото множество: (0, 0), (240, 0), (200, 80), (95, 150), (0, 150) Фигура 2.2).

Фигура 2.2: Допустимо множество и координати на върховете.

2.4 Целева функция и оптимален план

За да определим оптималния план графично ще начертаем прави, съответстващи на различни нива на печалба.

Фигура 2.3: Графично решение.

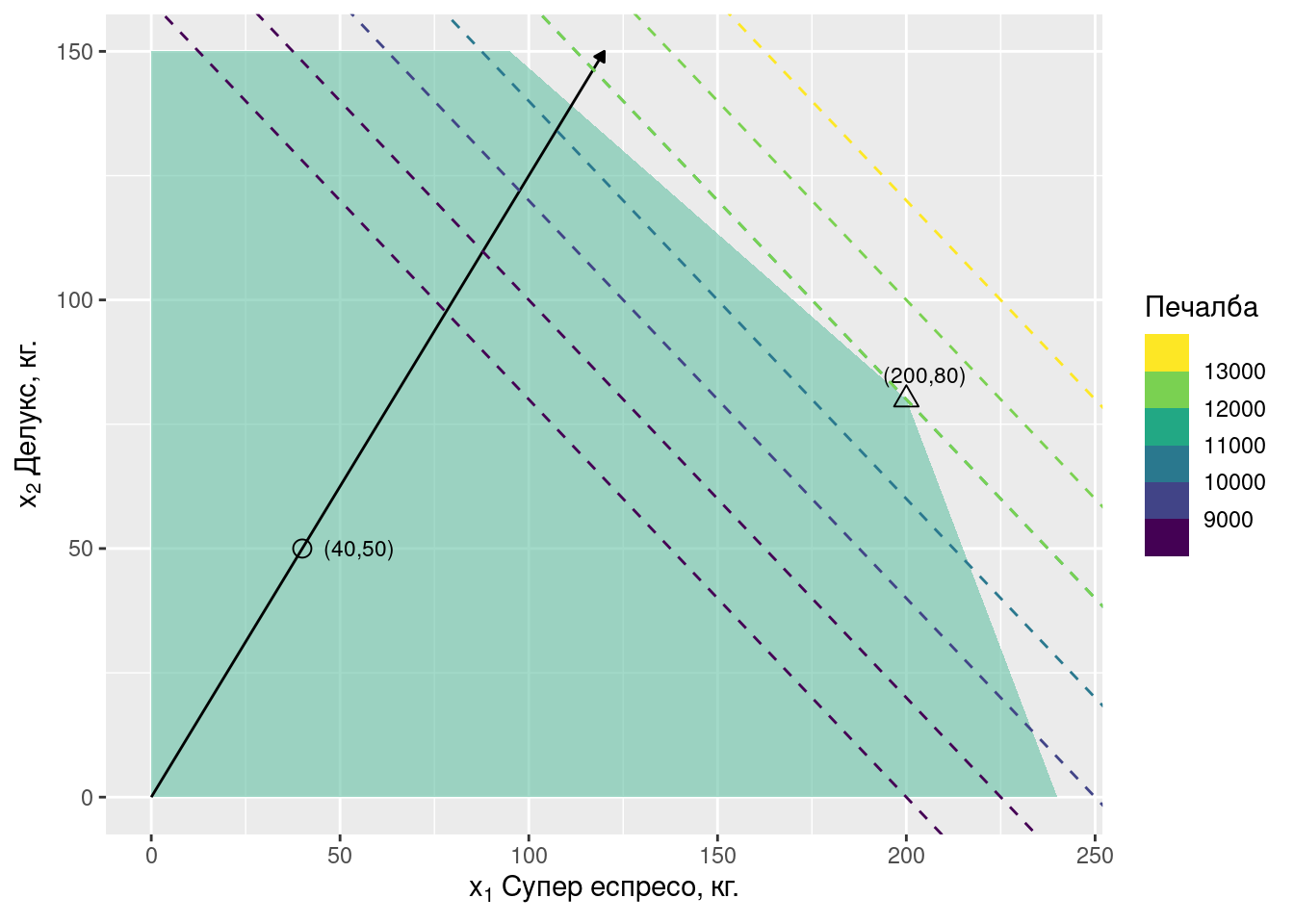
Всички комбинации \(x_1\) и \(x_2\), за които печалбата (целевата функция) е равна на 5000 лв лежат на права, определена от равенството:

\[ z = 40x_1 + 50x_2 = 5000 \]

Всички комбинации \(x_1\) и \(x_2\), за които печалбата (целевата функция) е равна на 1000 лв. лежат на права, определена от равенството

\[ z = 40x_1 + 50x_2 = 10000 \]

Двете прави са успоредни една спрямо друга, тъй като наклонът на правите зависи от коефициентите на \(x_1\) и \(x_2\) в уравненията и не зависи от константите (5 000 в първото уравнение и 10 000 във второто).

Векторът (40, 50) се нарича нормален вектор на правите на функцията на печалба и е перпендикулярен на тях. Координатите на нормалния вектор се получават от коефициентите на \(x_1\) и \(x_2\) в целевата функция.

Правата на максималната печалба (12 000 лв.) се допира до допустимото множество в точката \((x^*_1 = 200, x^*_2 = 80)\), която е и оптималният план.

2.5 Дефицитност на ресурси

В оптималния план \((x^*_1 = 200, x^*_2 = 80)\) заведението изразходва:

\[ \begin{aligned} 0.5 x^*_1 + 0.25 x^*_2 & = 0.5 \cdot 200 + 0.25 \cdot 80 & = 120 \text{ кг. бразилско кафе} \\ 0.5 x^*_1 + 0.75x^*_2 & = 0.5 \cdot 200 + 0.75 \cdot 80 & = 160 \text{ кг. кубинско кафе} \\ 0 \cdot x^*_1 + x^*_2 & = 0\cdot 200 + 1\cdot 80 & = 80 \text{ кг. търсене Делукс} \end{aligned} \]

Общо заведението разполага с 120 кг. бразилско кафе, 160 кг. кубинско кафе и 150 кг. търсене на Делукс. Тъй като в оптимума се изразходва цялото налично количество от кубинско и бразилско кафе казваме, че тези ресурси са дефицитни. Кои ресурси са дефицитни може да се види лесно от графиките. В пресечната точка на две прави едновременно са изпълнени и двете уравнения, които ги определят.

• Във всяка точка от правата на ограничението за бразилското кафе важи, че изразходваното количество бразилско кафе е 120 кг., защото е изпълнено Уравнение (eq:p-2-constr-brazilian).
• Във всяка точка от правата на ограничението за кубинското кафе важи, че изразходваното количество кубинско кафе е 120 кг., защото е изпълнено уравнението (eq:p-2-constr-cuban).
• Във всяка точка от правата на ограничението за търсене на Делукс важи, че изразходваното количество “търсене на Делукс” е 150 кг., защото е изпълнено Уравнение (eq:p-2-constr-demand).

В оптималния план остават \(150 - 80 = 70\) кг. неизползвано търсене на Делукс (slack). Казваме, че “търсенето на Делукс” е недефицитен ресурс.

2.6 Изчисления с R и Python (опционално)

Изчисляване на пресечните точки на правите:

# ## Constraints matrix
Constr <- matrix(
  c(
    0.5, 0.25,
    0.5, 0.75,
    0, 1
  ),
  nrow = 3,
  ncol = 2,
  byrow = TRUE
)

## Constraints RHS
RHS <- c(120, 160, 150)

## Brazilian/Cuban
solve(Constr[-3, ], RHS[-3])

[1] 200  80

## Brazilian/Demand
solve(Constr[-2, ], RHS[-2])

[1] 165 150

## Cuban/Demand
solve(Constr[-1, ], RHS[-1])

[1]  95 150

import numpy as np
from scipy import linalg

/home/amarov/anaconda3/lib/python3.9/site-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.16.5 and <1.23.0 is required for this version of SciPy (detected version 1.23.4
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

Constr = np.array([[0.5, 0.25], [0.5, 0.75], [0, 1]])
RHS = np.array([120, 160, 150])

# Brazilian/Cuban
linalg.solve(Constr[[0, 1],], RHS[[0, 1]])

# Brazilian/Demand

array([200.,  80.])

linalg.solve(Constr[[0, 2],], RHS[[0, 2]])

# Cuban/Demand

array([165., 150.])

linalg.solve(Constr[[1, 2],], RHS[[1, 2]])

array([ 95., 150.])

2.7 Допустими граници на промяна

• В какви граници може да се променя ограничението за бразилското кафе без да се промени характера на оптималния план (без да се променят дефицитните ресурси)?

• В какви граници може да се променя ограничението за кубинското кафе без да се промени характера на оптималния план (без да се променят дефицитните ресурси)?

• В какви граници може да се променя ограничението за търсенето на Супер еспресо кафе без да се промени характера на оптималния план (без да се променят дефицитните ресурси)?

За да видим как се променя решението на задачата, когато варираме наличното количество кубинско кафе, ще я решим графично при четири нива на наличност на ресурса: 120 кг., 180 кг., 195 кг. и 220 кг. Уравненията на ограниченията за всяко от тези нива са:

\[ \begin{aligned} 0.5 x_1 + 0.75 x_2 & = 160 \text{ налични 160 кг. (първоначална задача)} \\ 0.5 x_1 + 0.75 x_2 & = 180 \text{ налични 180 кг.} \\ 0.5 x_1 + 0.75 x_2 & = 220 \text{ налични 220 кг.} \\ 0.5 x_1 + 0.75 x_2 & = 195 \text{ налични 195 кг.} \\ \end{aligned} \]

Първото от тези нива е първоначалното ниво в задачата, която решихме използвайки Фигура 2.3.

За втория случай Фигура 2.4 показва решението при 180 кг. налично кубинско кафе. Оптималната комбинация от Супер и Делукс еспресо е (180, 120) при печалба от \(40 \cdot 180 + 50 \cdot 120 = 13200\) лв. Дефицитните ресурси отново са “бразилско кафе” и “кубинско кафе”, т.е. характерът на решението не се променя спрямо първоначалната задача.

Фигура 2.4: Допустимо множество и оптимум при 160 и при 180 кг. разполагаемо кубинско кафе.

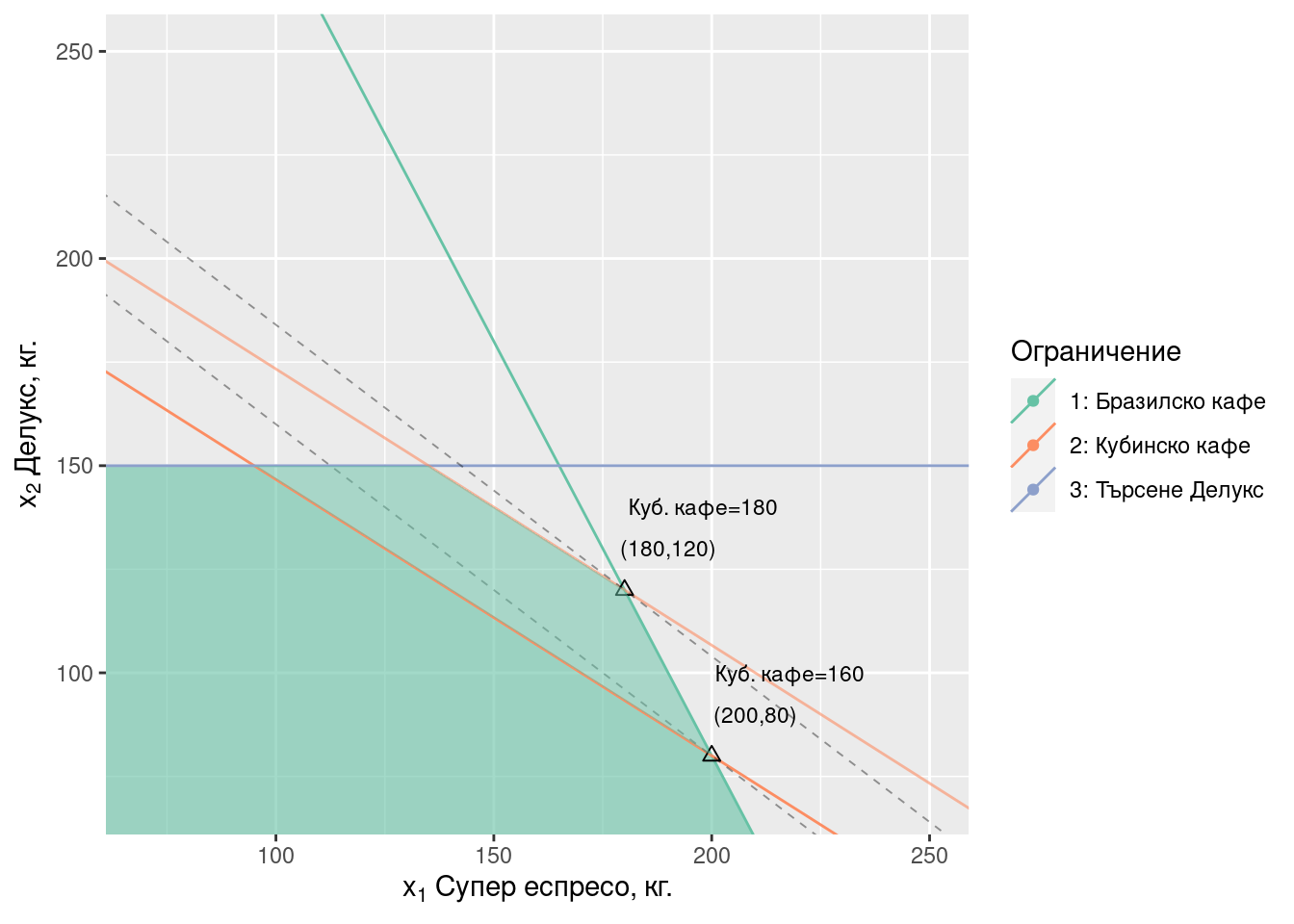
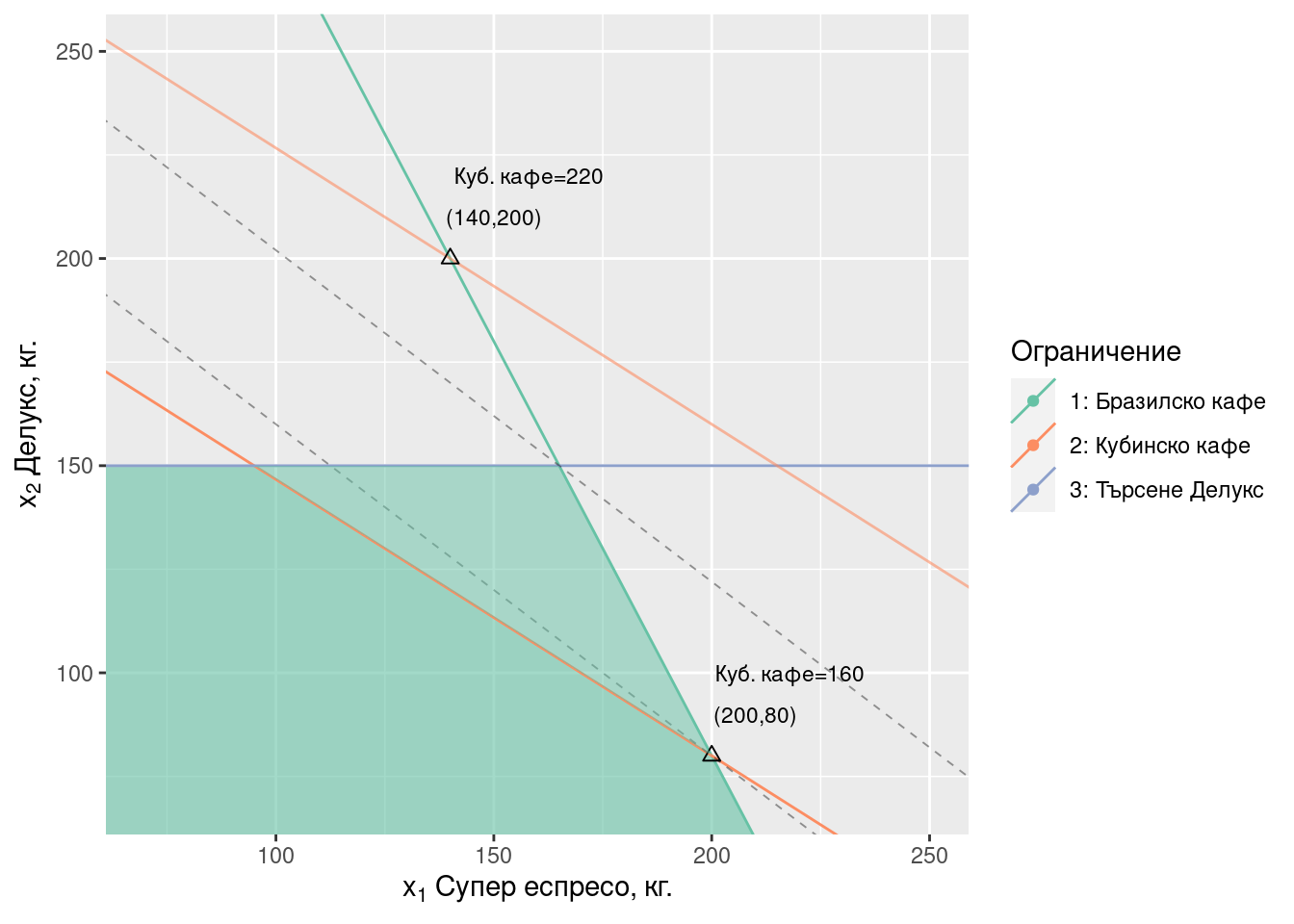
За третия случай Фигура 2.5 показва решението при 220 кг. налично кубинско кафе. Пресечната точка на правите към “бразилско кафе” и “кубинско кафе” при (140, 200) този път не е оптимален план, защото не принадлежи към допустимото множество, тъй като не изпълнява ограничението за търсене на Делукс (\(200 \nleq 150\)).

От графиката виждаме, че при наличие на кубинско кафе от повече от 195 кг. се променя характера на оптимума, защото дефицитни стават ресурсите “бразилско кафе” и “търсене Делукс”. Разликата между 195 кг. и първоначално наличните в задачата 160 кг. наричаме допустимо увеличение на ресурса (195 - 160 = 35 кг.). Новият оптимум е пресечната точка на “бразилско кафе” и “търсене Делукс”. Можем да намерим координатите на тази точка като решение на системата от двете уравнения (eq:p-2-constr-brazilian) и (eq:p-2-constr-demand):

\[ \begin{equation} \left | \begin{array}{@{}l@{}} 0.5 x_1 + 0.25 x_2 & = 120 \\ 0 \cdot x_1 + x_2 & = 150 \end{array}\right.\,. \end{equation} \]

Решението на системата е (165, 150). За разлика от оптимумите при 160 кг. и 180 кг. кубинско кафе, сега дефицитните ресурси са “бразилско кафе” и “търсене Делукс”.

Фигура 2.5: Допустимо множество и оптимум 160 и при 220 к. разполагаемо кубинско кафе.

В четвъртия случай при наличие на 195 кг. кубинско кафе допустимото множество съвпада с това в предходня пример при 220 кг. Фигура 2.6. По тази причина и оптимумът е същият: (165, 150) при ниво на печалба \(40 \cdot 165 + 50 \cdot 150 = 14100\) лв.

Фигура 2.6: Допустимо множество и оптимум при 160 и при 195 кг. разполагаемо кубинско кафе.

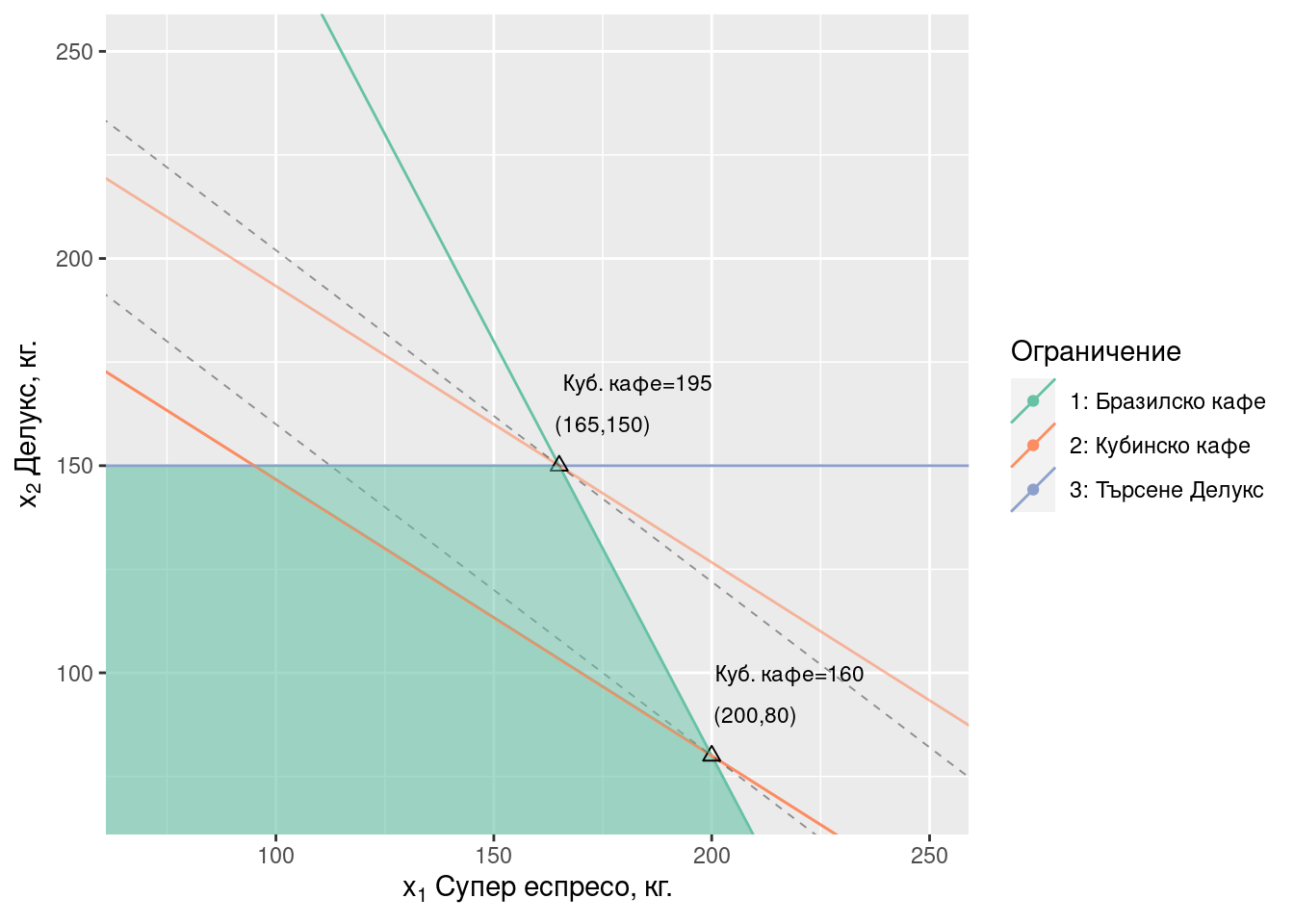
От тези примери виждаме, че количеството кубинско кафе може да се увеличи с най-много \(195 - 160 = 35\) кг. без да се промени характера на оптимума. Това количество наричаме допустимо увеличение (allowable increase).

2.8 Скрити цени

В предходната секция изчислихме, че можем да увеличим наличността от бразилско кафе до 195 кг. без това да промени характера на решението. Максималната печалба при \(x_1 = 165, x_2 = 150\) e

\[ z = 40 \cdot 165 + 50 \cdot 150 = 1.41\times 10^{4}. \]

Тази по-висока печалба можем да постигнем за сметка на \(195 - 160 = 35\) кг. допълнително кубинско кафе. Съотношението между допълнителната печалба и допълнителното количество кафе наричаме скрита цена на (кубинското) кафе:

\[ \frac{\Delta z^*}{\Delta r^*} = \frac{z^{*1} - z^{*}}{r^{*1} - r^{*}} = \frac{1.41\times 10^{4} - 1.2\times 10^{4}}{195 - 160} = \frac{2100}{35} = 60. \]

• Доставчикът предлага да достави допълнителни 10 кг. кубинско кафе на цена от 20 лв./кг. Бихте ли препоръчали на заведението да приеме тази оферта?

• Съседно заведение предлага да купи 5 килограма от бразилското кафе на цена 40 лв./кг. Изгодно ли е за заведението да продаде това количество кафе?

• Мениджърът на заведението предлага да въведе нов продукт, който предполага, че ще може да продава на цена не по-малка от 6 лв./кг. За производството на един килограм от този нов продукт са нужни 0.7 кг. бразилско и 0.3 кг. кубинско кафе. Бихте ли препоръчали на фирмата да започне това производство?

2.9 Реализация в Excel

Тук можете да изтеглите пример за реализация в Excel.

Съдържание на “Answer report”

Таблица 2.1: Целева функция

Cell	Name	Original Value	Final Value
$E$3	Order Profit	0	12000

Таблица 2.2: Целеви променливи

Cell	Name	Original Value	Final Value	Integer
$B$3	Order Super	0	200	Contin
$C$3	Order Delux	0	80	Contin

Таблица 2.3: Ограничения

Cell	Name	Cell Value	Formula	Status	Slack
$D$7	Brazilian Used	120	$D$7<=$E$7	Binding	0
$D$8	Cuban Used	160	$D$8<=$E$8	Binding	0
$D$9	Demand Used	80	$D$9<=$E$9	Not Binding	70

Съдържание на анализа на чувствителността (sensitivity report).

Таблица 2.4: Анализ на чувствителността: целеви променливи.

Cell	Name	Final value	Reduced Cost	Objective Coefficient	Allowable Increase	Allowable Decrease
$B$3	Order Super	200	0	40	60	6.666667
$C$3	Order Delux	80	0	50	10	30.000000

Таблица 2.5: Анализ на чувствителността: ограничения.

Cell	Name	Final value	Reduced Cost	Objective Coefficient	Allowable Increase	Allowable Decrease
$D$7	Brazilian Used	120	20	120	4.0e+01	35
$D$8	Cuban Used	160	60	160	3.5e+01	40
$D$9	Demand Used	80	0	150	1.0e+30	70

2.10 Реализация в R (опционално)

A <- matrix(
  c(
    1 / 2, 1 / 4,
    1 / 2, 3 / 4,
    0, 1
  ),
  ncol = 2,
  byrow = TRUE
)
b <- c(40, 50)
r <- c(120, 160, 150)

f.dir <- rep("<=", nrow(A))

lp_res <- lpSolve::lp(
  direction = "max",
  objective.in = b,
  const.mat = A,
  const.dir = f.dir,
  const.rhs = r
)

cat("Objective:", lp_res$objval, "\n")

Objective: 12000 

cat("Using x1 =", lp_res$solution[1], "x2 =", lp_res$solution[2], "\n")

Using x1 = 200 x2 = 80 

2.11 Реализация в Python (опционално)

from pulp import *

model = LpProblem("Coffee mix", LpMaximize)

# Define variables

/home/amarov/anaconda3/lib/python3.9/site-packages/pulp/pulp.py:1352: UserWarning: Spaces are not permitted in the name. Converted to '_'
  warnings.warn("Spaces are not permitted in the name. Converted to '_'")

Super = LpVariable("Super", lowBound=0)
Deluxe = LpVariable("Deluxe", lowBound=0)

# Objective function
model += 40 * Super + 50 * Deluxe

# Constraint: Brazilian
model += 0.5 * Super + 0.25 * Deluxe <= 120, "бразилско кафе"

# Constraint: Cuban
model += 0.5 * Super + 0.75 * Deluxe <= 160, "кубинско кафе"

# Constraint: demand
model += Deluxe <= 150, "търсене на Делукс"

# Solve the model
model.solve()

# Print the model status

1

print("Model Status:{}".format(LpStatus[model.status]))

# Print the value of the objective function at the optimal solution

Model Status:Optimal

print("Objective =", value(model.objective))

# Print the value of each variable at the optimal solution

Objective = 12000.0

for v in model.variables():
  print(v.name, "=", v.varValue)

Deluxe = 80.0
Super = 200.0

for name, c in model.constraints.items():
  print("Constraint: {}, shadow price: {}, slack {}".format(name, c.pi, c.slack))
  
# Print the model status

Constraint: бразилско_кафе, shadow price: 20.0, slack -0.0
Constraint: кубинско_кафе, shadow price: 60.0, slack -0.0
Constraint: търсене_на_Делукс, shadow price: -0.0, slack 70.0

print("Model Status:{}".format(LpStatus[model.status]))

# Print the value of the objective function at the optimal solution

Model Status:Optimal

print("Objective =", value(model.objective))

# Print the value of each variable at the optimal solution

Objective = 12000.0

for v in model.variables():
  print(v.name, "=", v.varValue)

Deluxe = 80.0
Super = 200.0

for name, c in model.constraints.items():
  print("Constraint: {}, shadow price: {}, slack {}".format(name, c.pi, c.slack))

Constraint: бразилско_кафе, shadow price: 20.0, slack -0.0
Constraint: кубинско_кафе, shadow price: 60.0, slack -0.0
Constraint: търсене_на_Делукс, shadow price: -0.0, slack 70.0

2.12 Пример (2)

Фирма произвежда два вида месингови изделия – А и Б и разполага с 600 kWh електроенергия, 480 кг. мед и 750 кг. цинк. Разходите за електроенергия и метали са дадени в Таблица 2.6. Печалбата от единица продукт е една и съща и за двете изделия. Определете (графично) допустимото множество и оптималния производствен план.

Таблица 2.6: Технологична таблица

Ресурс	А	Б
Ел. енергия	3	3
Мед	3	2
Цинк	4	1

2.12.1 Допустимо множество

\[ \begin{align*} x_1: \text{брой единици от продукт А}\\ x_2: \text{брой единици от продукт Б} \end{align*} \] \[ \begin{align*} 3 x_1 + 3 x_2 & \leq 600 \text{ (ел. енергия)}\\ 3 x_1 + 2 x_2 & \leq 480 \text{ (мед)}\\ 4 x_1 + 1 x_2 & \leq 750 \text{ (цинк)}\\ x_1 \geq 0 \\ x_2 \geq 0 \end{align*} \]

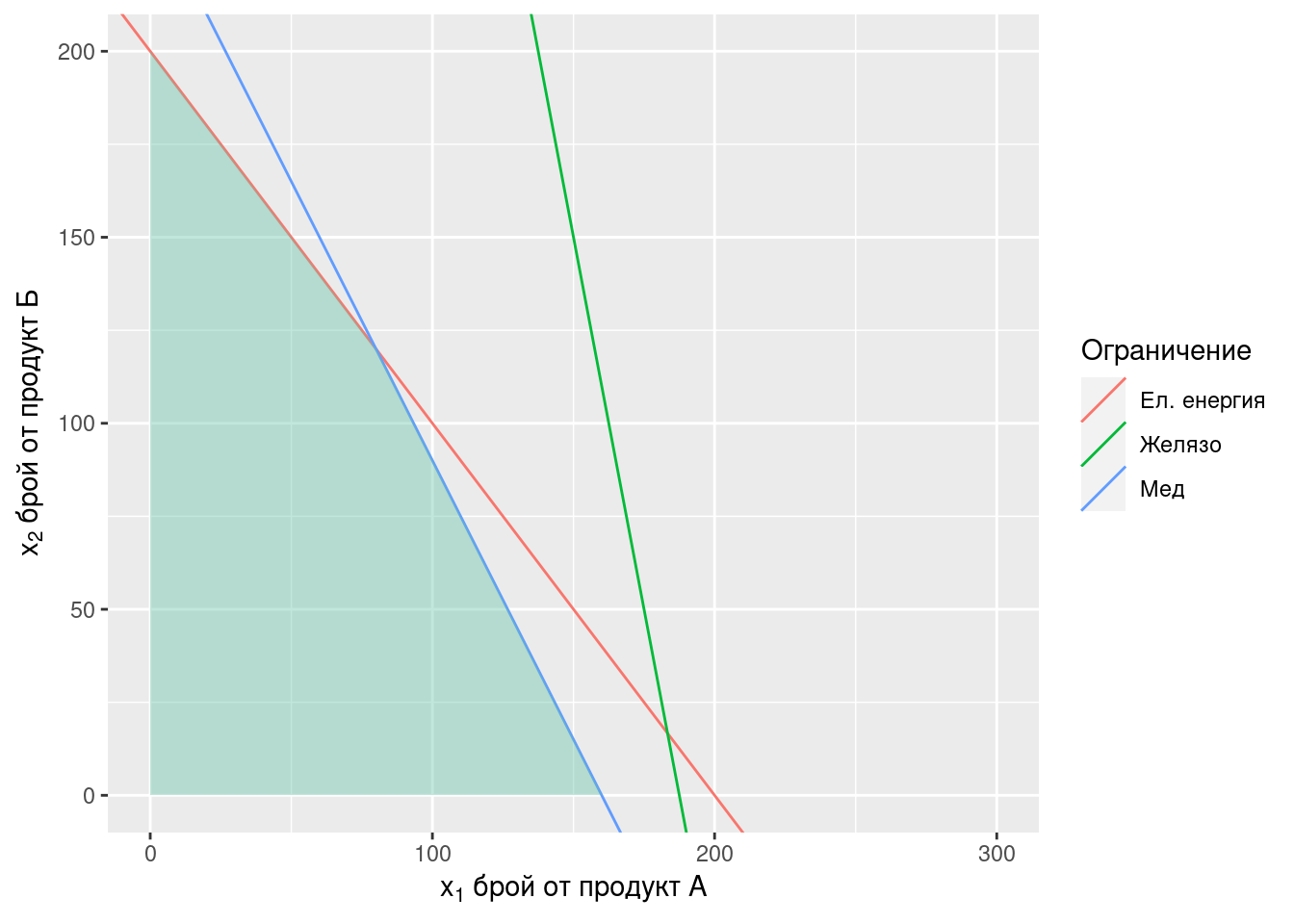
Допустимото множество е полигонът с върхове: (0, 0), пресечната точка на “мед” и оста \(x_1\): (160, 0), пресечната точка на “мед” и “ел. енергия” и пресечната точка на “ел. енергия” с оста \(x_2\).

Пресечната точка на “мед” и “ел. енергия” можем да намерим, като решим системата уравнения

\[ \begin{align} 3 x_1 + 3 x_2 & = 600\\ 3 x_1 + 2 x_2 & = 480. \end{align} \]

В предходния пример намерихме пресечната точка на правите към две ограничения като решихме система от две уравнения (като извадихме едното уравнения от другото). Тук ще решим тази система от уравнения с правилото на Крамер, за да го илюстрираме (двата подхода са еквивалентни):

2.13 Формули на Крамер

За система от линейни уравнения

\[ \begin{equation} \left | \begin{array}{@{}l@{}} a_{11} x_1 + a_{12} x_2 & = b_1 \\ a_{21} x_1 + a_{22} x_2 & = b_2 \end{array}\right.\,, \end{equation} \] решението на системата (ако съществува едно решение) е дадено от:

\[ \begin{align} x^*_1 = \frac{\Delta_1}{\Delta}\\ x^*_2= \frac{\Delta_2}{\Delta} \end{align} \] където \(\Delta_1\), \(\Delta_2\) и \(\Delta\) са детерминантите:

\[ \Delta = \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{22} & a_{22} \end{array} \right|, \Delta_1 = \left | \begin{array}{cc} b_1 & a_{21} \\ b_2 & a_{22} \end{array} \right |, \Delta_2 = \left | \begin{array}{cc} a_{11} & b_1 \\ a_{21} & b_2 \end{array} \right |.\, \]

Ако \(\Delta = 0\), тогава двете уравнения в системата са линейно зависими, което означава, че правите, дефинирани от уравненията са успоредни.

Приложено в конкретния пример получаваме:

\[ \begin{align} \Delta & = \left| \begin{array}{cc} 3 & 3 \\ 3 & 2 \end{array} \right| = 3 \cdot 2 - 3 \cdot 3 = 6 - 9 = -3 \\ \Delta_1 & = \left | \begin{array}{cc} 600 & 3 \\ 480 & 2 \end{array} \right | = 600 \cdot 2 - 3 \cdot 480 = -240 \\ \Delta_2 & = \left | \begin{array}{cc} 3 & 600 \\ 3 & 480 \end{array} \right | = 3 \cdot 480 - 600 \cdot 3 = -360 \implies\\ x^*_1 & = \frac{\Delta_1}{\Delta} = \frac{-240}{-3} = 80 \\ x^*_2 & = \frac{\Delta_2}{\Delta} = \frac{-360}{-3} = 120. \end{align} \]

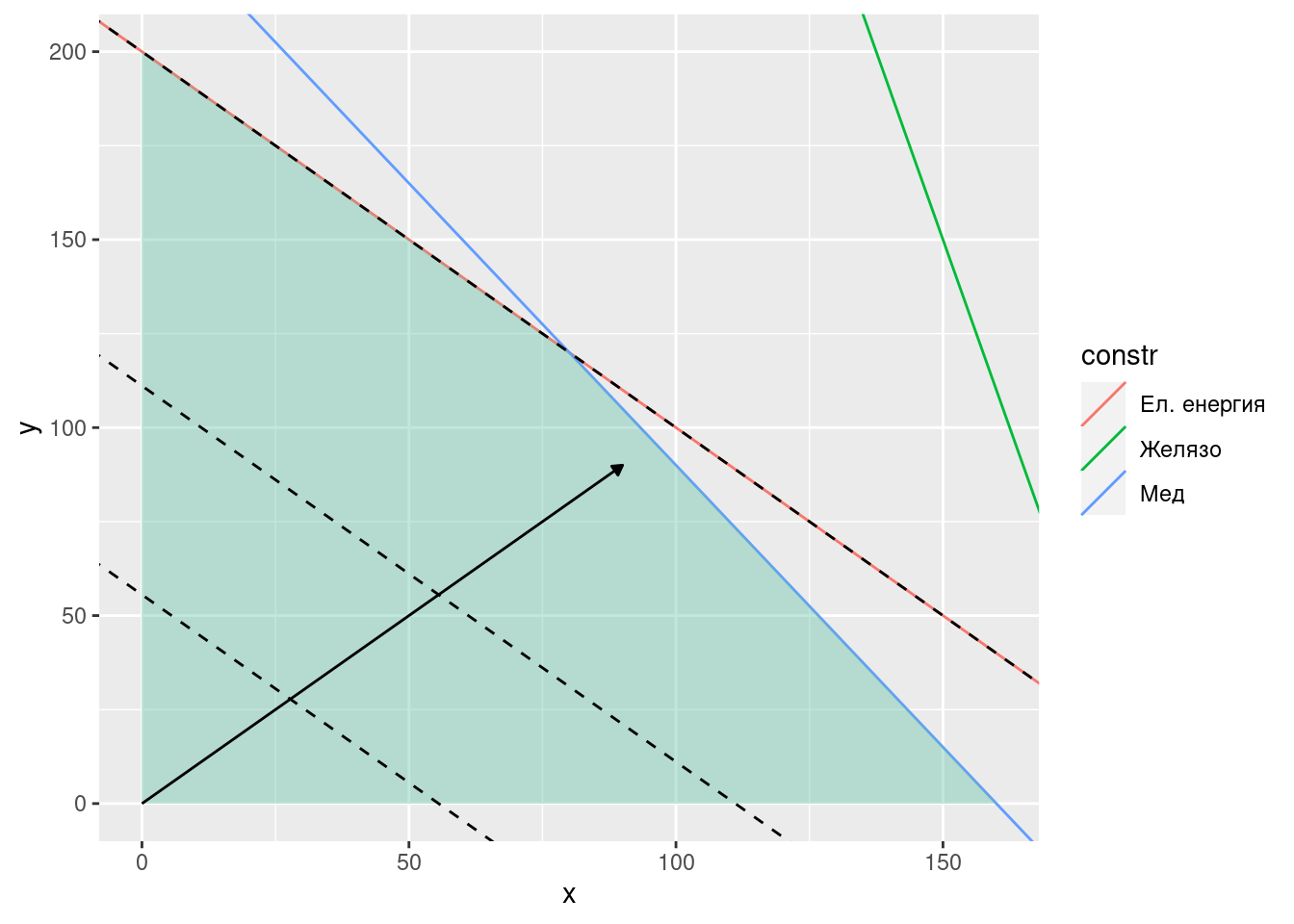
Оптимални са всички комбинации от \(x_1\) и \(x_2\), които лежат на отсечката между \((0, 200)\) и \((80, 120)\):

\[ \left( \begin{array}{c} x^*_1 \\ x^*_2 \end{array} \right) = \alpha \left(\begin{array}{c} 0 \\ 200 \end{array}\right) + (1 - \alpha) \left(\begin{array}{c} 80 \\ 120 \end{array}\right), \quad 0 \geq \alpha \leq 1 \]

2.14 Пример (3)

Намерете решението на следната задача:

\[ \max z = 8x_1 + 6 x_2\\ 5 x_1 + 4 x_2 \leq 60\\ 2 x_1 + 4 x_2 \leq 48 \\ 3 x_2 \geq 60 \\ x_1 \geq 0\\ x_2 \geq 0 \]

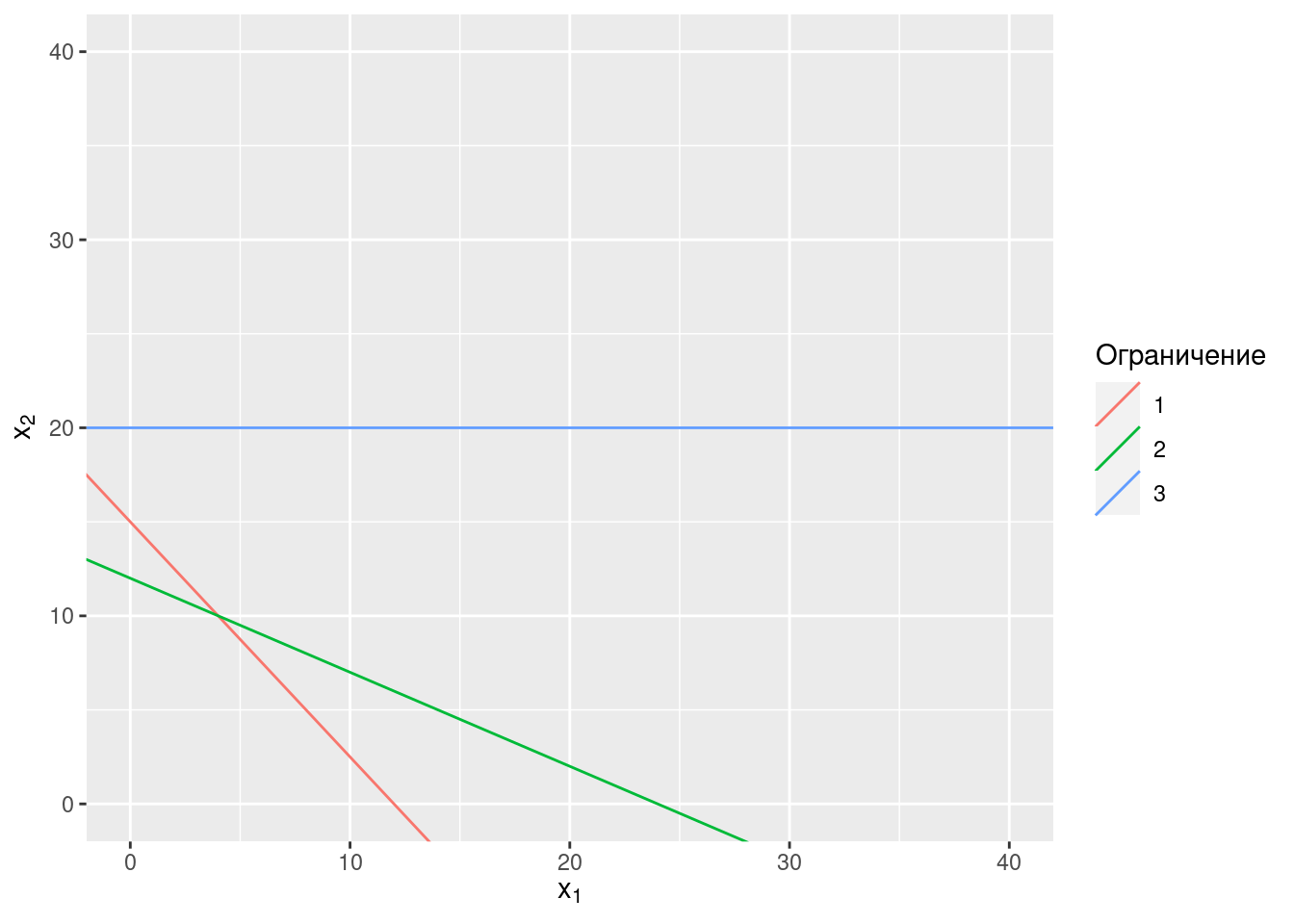
2.15 Пример (5)

Намерете решението на следната задача:

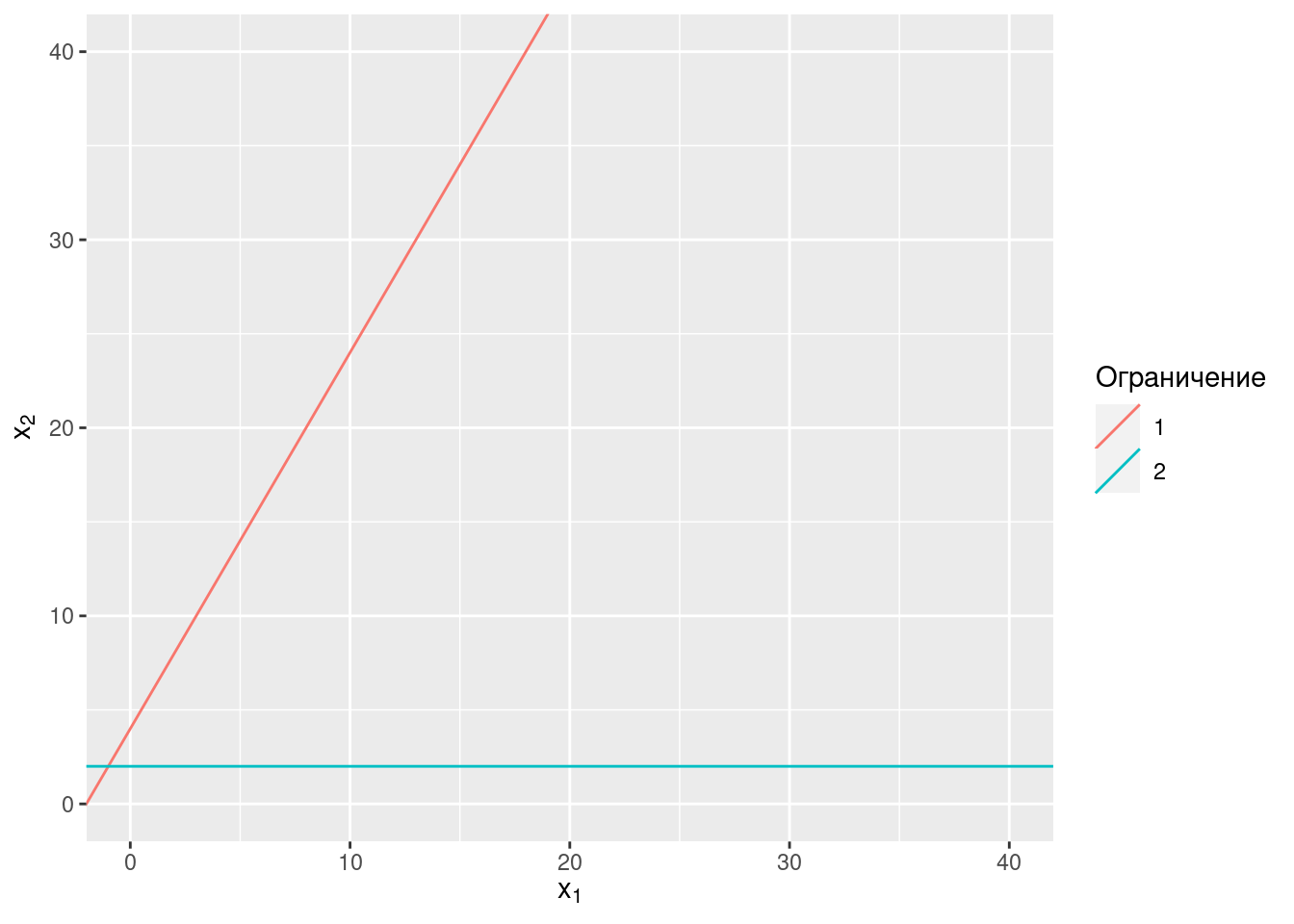
\[ \max z = 3x_2 \\ -2 x_1 + x_2 \leq 4 \\ x_2 \geq 2 \\ x_1 \geq 0\\ x_2 \geq 0 \]